Parameter calibration of a discrete element simulation model for dry lightweight heterogeneous media
-
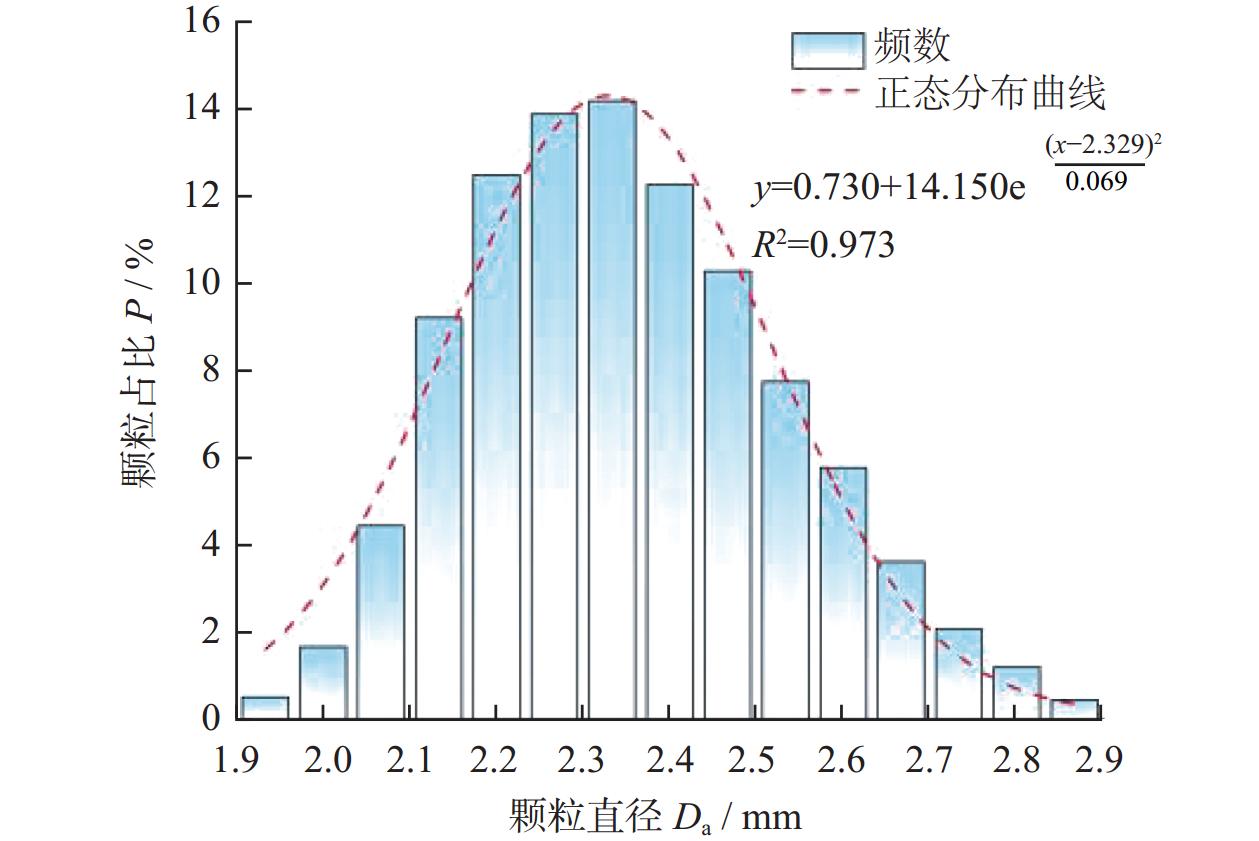
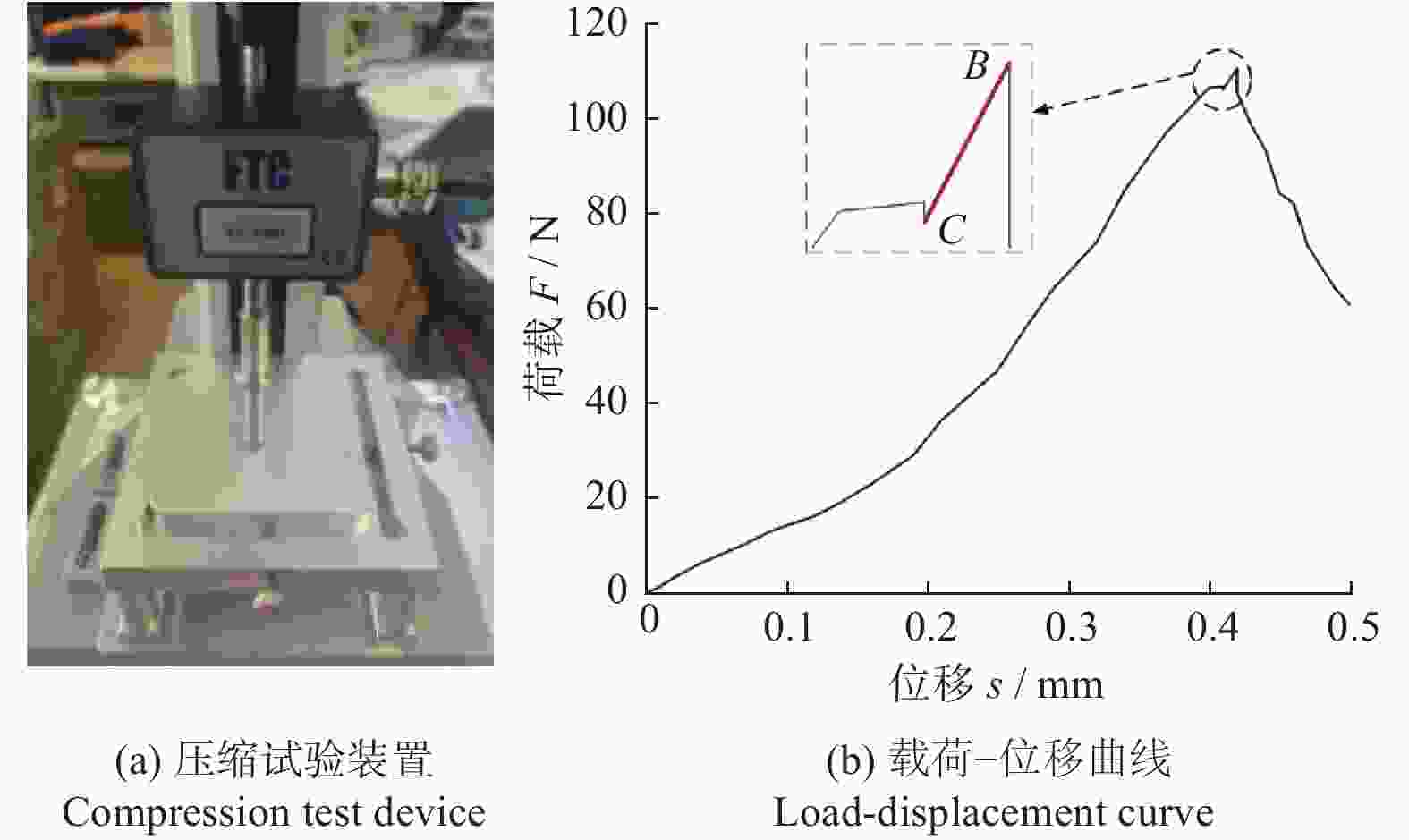
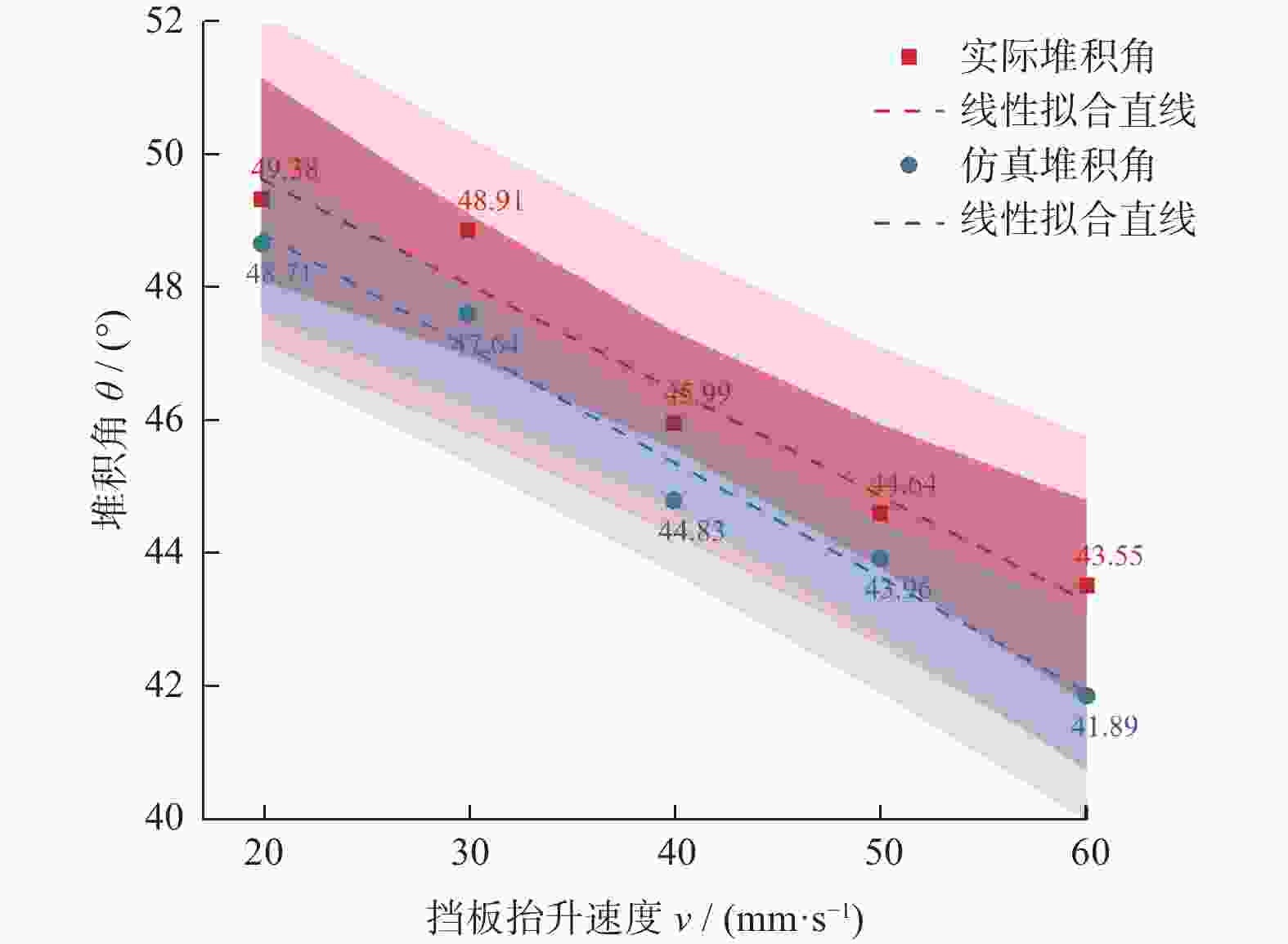
摘要: 干式轻质异形介质是滚磨光整加工中常用的一类加工介质，其形状各异，导致离散元仿真中所使用的接触参数难以测试与标定，影响仿真模拟的准确性。以核桃壳介质为研究对象，首先通过物理试验测得核桃壳介质的几何形态、密度以及弹性/剪切模量等本征参数，其次采用自制的接触参数测量装置获得核桃壳介质与亚克力板间的静摩擦系数、滚动摩擦系数、碰撞恢复系数及核桃壳介质间的碰撞恢复系数，最后基于不同形状的特征参数，采用多维法构建出24种干式异形介质单颗粒仿真模型，并以实际堆积角为目标进行寻优，开展2因素5水平旋转正交组合仿真模拟试验，获得核桃壳介质间的静摩擦系数和滚动摩擦系数的最佳参数组合：静摩擦系数为0.829、滚动摩擦系数为0.191。采用测试及标定的本征参数和接触参数进行不同挡板抬升速度下的堆积角仿真，并与试验结果对比，最大相对误差＜4%。Abstract:
Objectives Dry light-shaped medium is a type of machining medium commonly used in the rolling finishing process. Its shape varies, making it difficult to test and calibrate the contact parameters used in discrete element simulation, which affects the accuracy of the simulation. In this study, walnut shell medium is taken as the research object, and the intrinsic parameters and contact parameters of walnut shell medium are tested based on the basic parameter measurement methods of granular material, both domestically and internationally. The friction coefficient between the medium is calibrated with the accumulation angle obtained by the experiment as the response value, in order to provide parameter support for the discrete element simulation of dry light-shaped medium roller grinding. Methods The density of walnut shell medium is obtained using oil discharge method and the measuring cylinder method. The elastic/shear modulus is measured by the texture analyzer. The shape characteristic parameters are measured by the PartAn 3D particle dynamic image analyzer, and the shapes are classified by the multi-dimensional method. Based on the strong correlation between two-dimensional and three-dimensional shape characteristic parameters, a single particle simulation model of 24 types of dry-shaped media is constructed, and the dry-shaped media are bonded into particle plates. The collision recovery coefficient between the dry-shaped media is measured by the inclined plate collision experiment. The static friction coefficient, rolling friction coefficient, and collision recovery coefficient between the dry-shaped medium and acrylic are obtained using a self-made contact parameter measuring device. Taking the actual packing angle as the test object and the friction coefficient between the walnut shell media as the factor, a two-factor five-level rotation orthogonal test is carried out to establish the second-order regression equation of the friction coefficient and packing angle. The actual packing angle, as the target value, is optimized. The discrete element simulation and experiment are combined to determine the best parameter combination of the static friction coefficient and the dynamic friction coefficient between the dry-shaped media. Results (1) The physical experiment results show that the real density of walnut shell medium is 1024 kg/m3, the packing density is 642 kg/m3, and the shear modulus is 9.219 × 107 Pa. (2) The collision recovery coefficient between the walnut shell medium and the acrylic plate is 0.246, the static friction coefficient is 0.422, the rolling friction coefficient is 0.175 and the collision recovery coefficient between the walnut shell medium is 0.340. (3) The actual stacking angle is the target value for optimization, and the optimal parameter combination of friction coefficient between dry-shaped media is determined by combining discrete element simulation and experiment: the static friction coefficient between walnut shell media is 0.829, and the rolling friction coefficient is 0.191. (4) The stacking test is carried out on the stacking angle under different baffle lifting speeds, and the relative error between the simulated and actual stacking angle is less than 4%, which proves that the parameter combination can be effectively used for EDEM simulation process analysis.Conclusions In this paper, the relevant parameters of walnut shell medium are measured and calibrated by combining experiment and simulation. Based on the multidimensional shape classification and the strong correlation between two-dimensional and three-dimensional morphological features, a single particle simulation model of dry-shaped medium can be effectively constructed. In this way, the calibrated walnut shell medium particle model can more truly simulate the interaction between walnut shell medium, parts, and processing equipment, and analyze and predict from a microscopic point of view. In the future, this method can be used for parameter testing and calibration of shaped media such as corncob and olive shell, thereby expanding the application range of the dry-shaped media calibration method. -
图 4 核桃壳介质的形状参数分布
Figure 4. Shape parameter distribution of walnut shell particles medium
图 5 真实密度测量试验装置
1—精密天平（精度：0.001 g）；2—100 mL量筒。
Figure 5. True density measuring test device
图 8 静摩擦系数测试装置
1—斜板；2—倾角仪；3—连杆；4—万向节；5—伺服电机；6—支撑座；7—丝杆；8—滑轨；9—滑块；10—铝制连接台。
Figure 8. Static friction coefficient test device
图 12 实际堆积角测量装置
1—料箱；2—挡板；3—锁紧螺母；4—固定轴丝杆步进电机；5—外箱。
Figure 12. Actual stacking angle measuring device
图 15 多维法划分形状参数区间
Figure 15. Multidimensional method to divide shape parameter interval
图 16 二维长宽比与三维延伸率之间的关系
Figure 16. Relationship between two-dimensional aspect ratio and three-dimensional elongation
图 17 二维圆形度与三维球形度之间的关系
Figure 17. Relationship between two-dimensional circularity medium and three-dimensional sphericity
图 18 核桃壳介质仿真模型的建立
Figure 18. Establishment of simulation model of walnut shell particles
图 20 核桃壳介质间静摩擦系数与滚动摩擦系数的响应曲面图
Figure 20. Response surface diagram of static fiction coefficient and rolling friction coefficient between walnut shell particle medium
图 21 不同抬升速度下仿真与实际堆积角数值对比
Figure 21. Comparison of simulation and physical stacking angle values at different lifting speeds
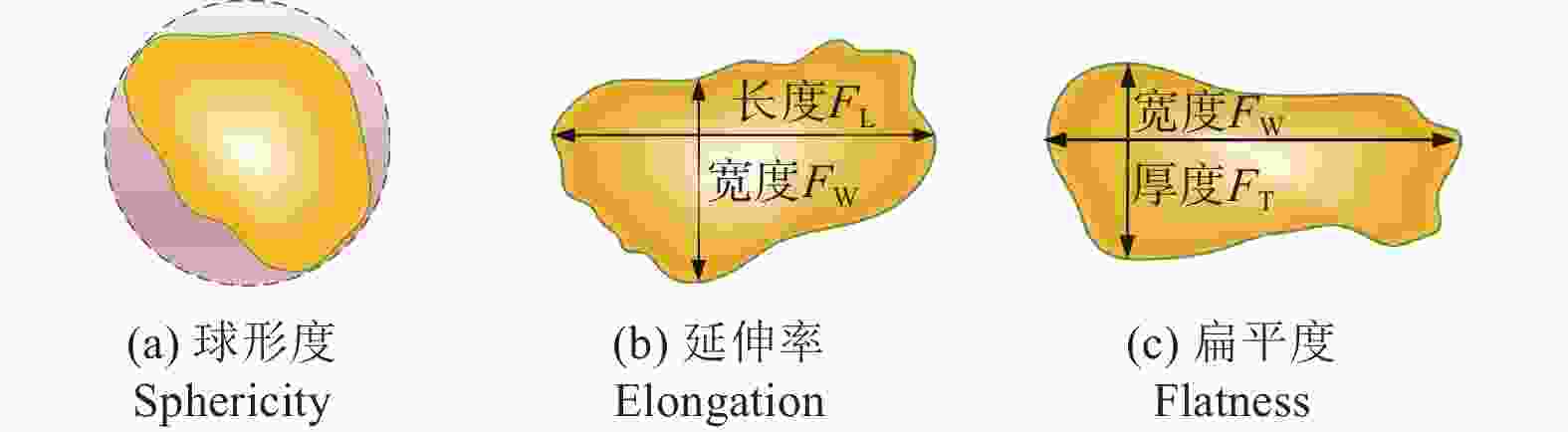
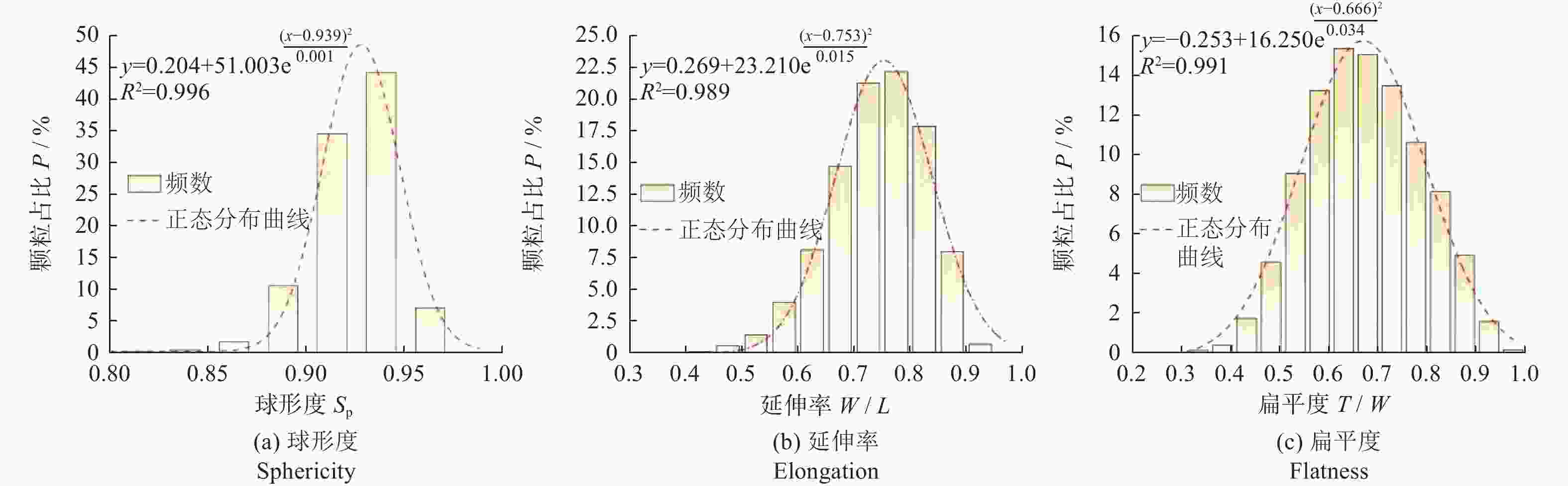
表 1 形状评定参数
Table 1. Shape evaluation parameter
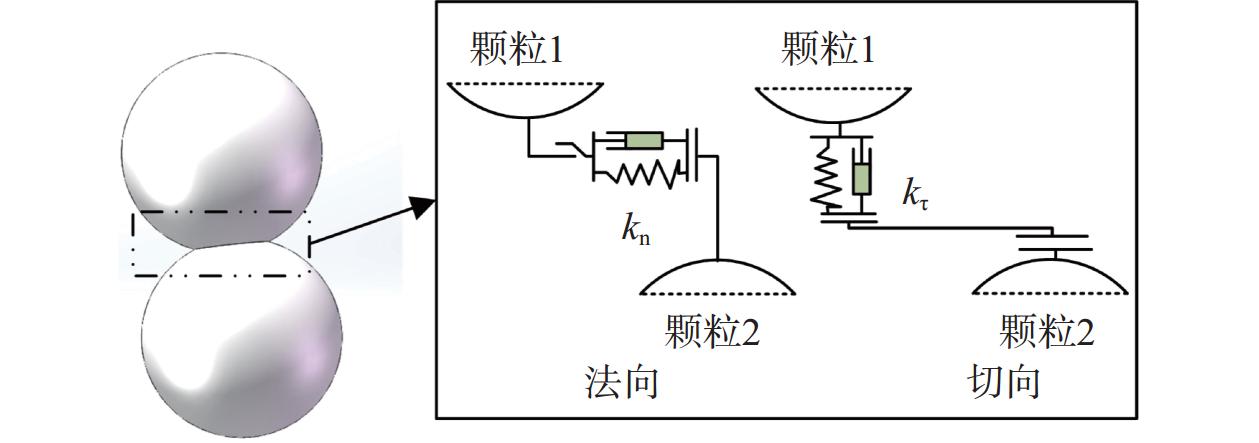
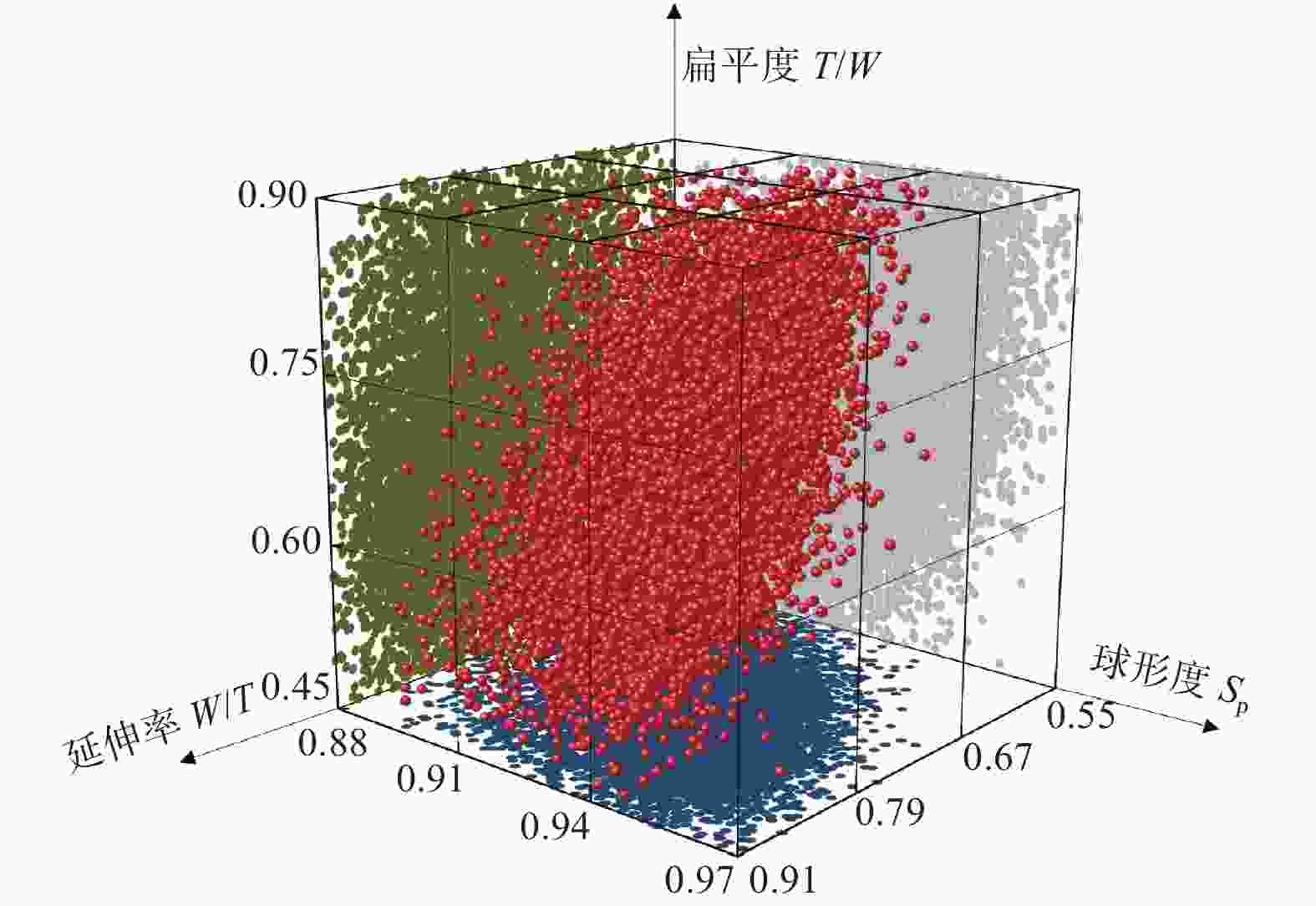
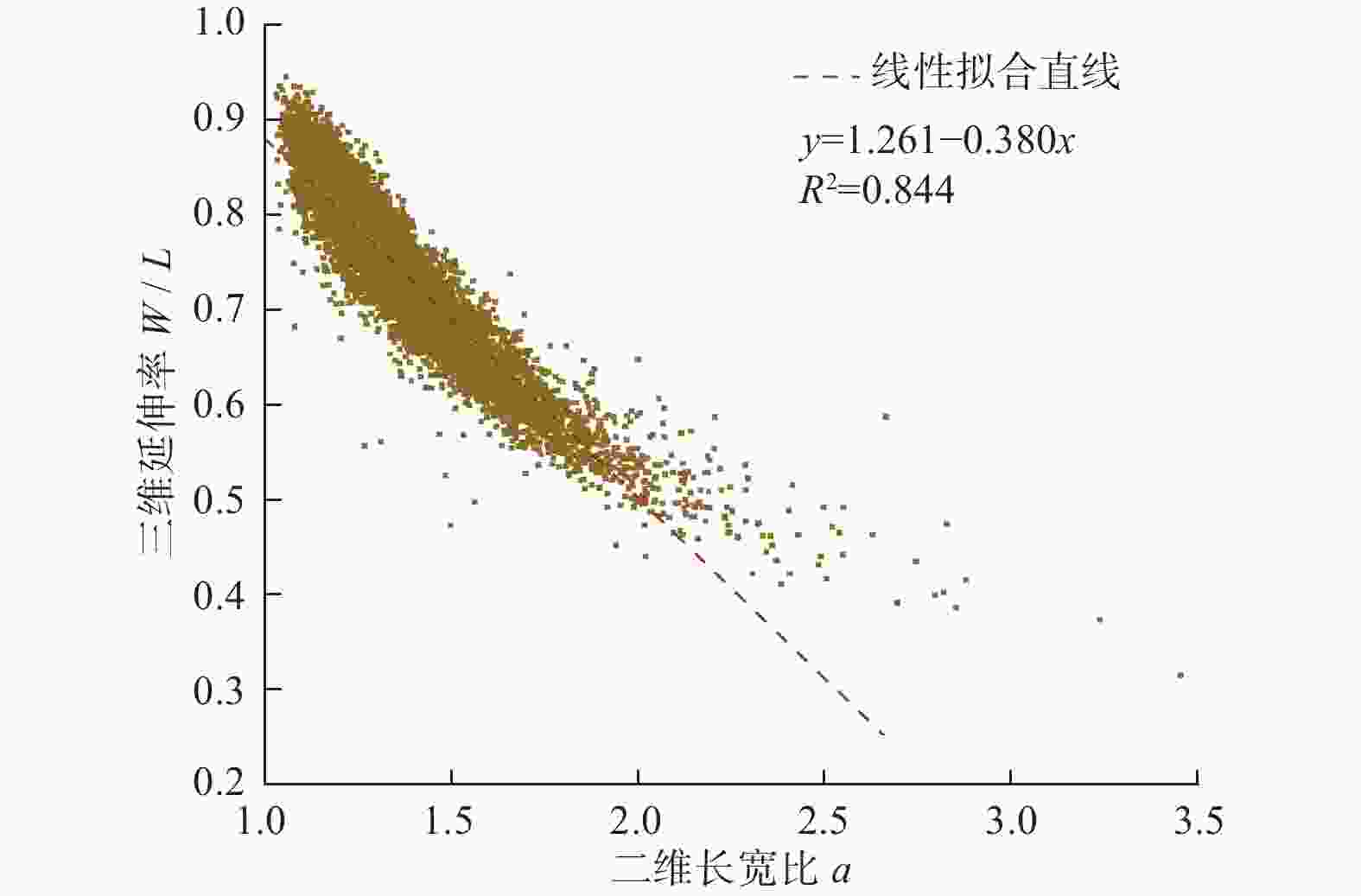
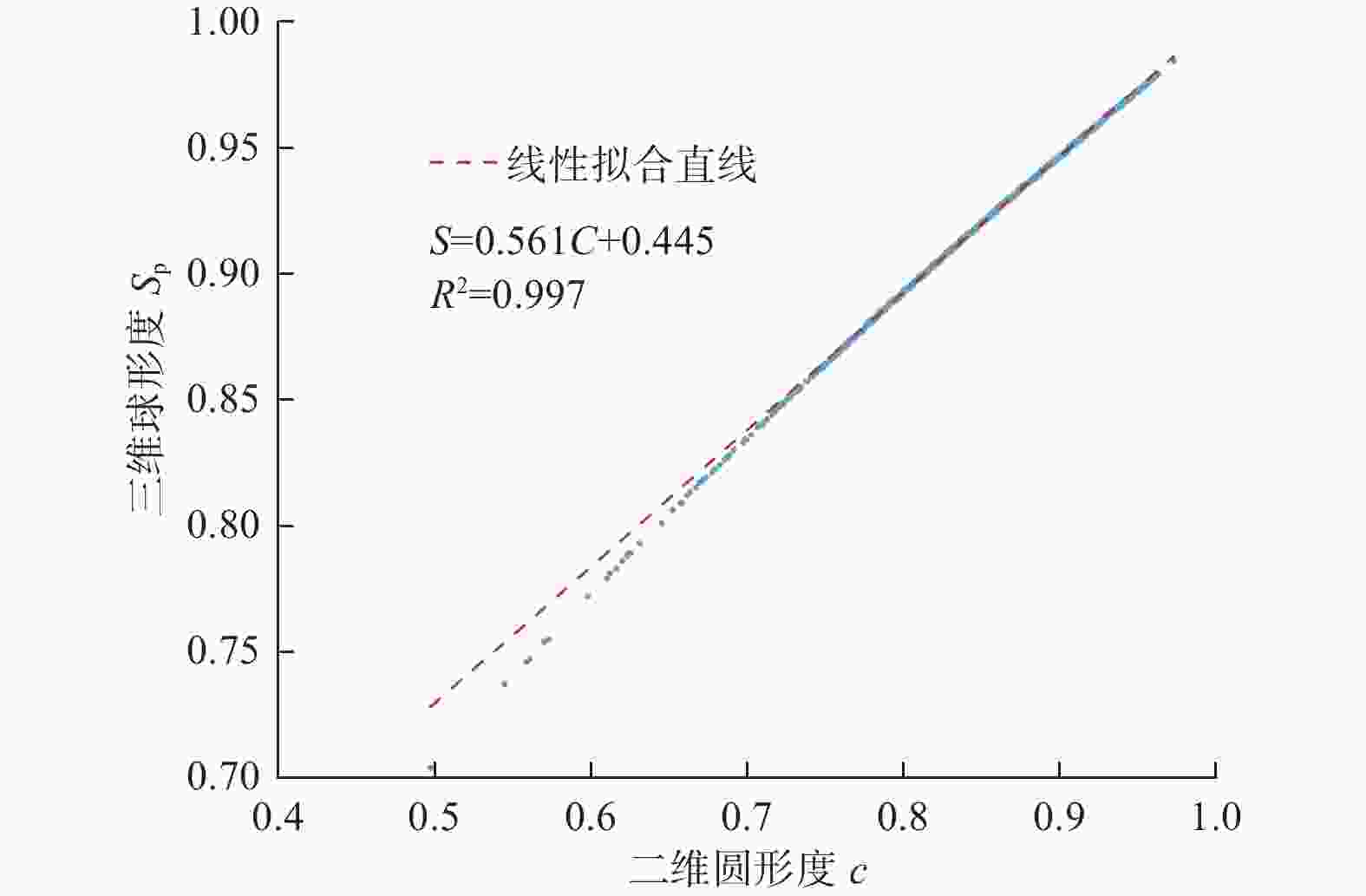
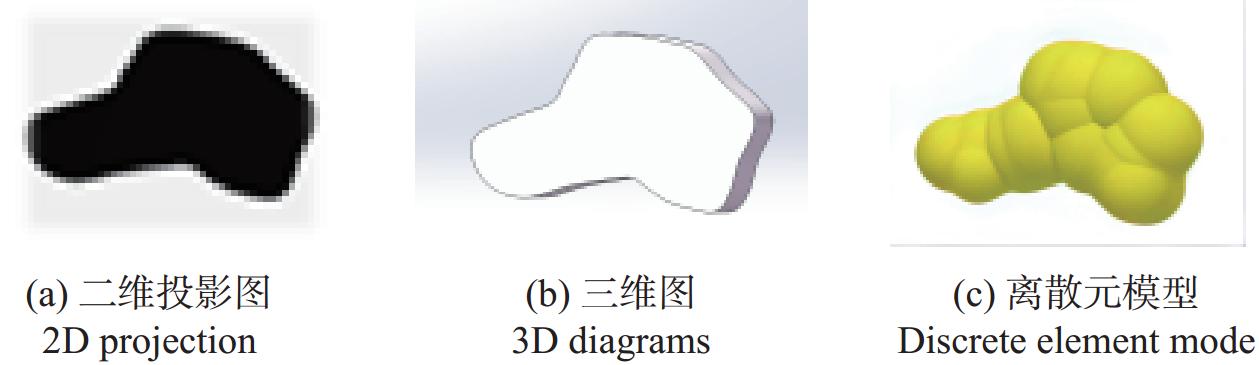
参数 定义 描述特征 球形度Sp Da / Dp 描述颗粒的近球形程度 延伸率W/L FW / FL 描述颗粒的狭长程度 扁平度T/W FT / FW 描述颗粒的扁平程度 注：Da为介质一系列投影图像等面积圆直径的均值；Dp为介质一系列投影图像等周长圆直径的均值；FW、FL和FT分别为介质的长度、宽度和厚度。 
下载: 导出CSV
表 2 核桃壳介质仿真模型
Table 2. DEM model of walnut shell particles medium
序号 1 2 3 4 5 6 7 8 9 $ \overline S_{\mathrm{p}} $ 0.895 0.895 0.895 0.895 0.895 0.895 0.895 0.895 0.895 $\overline {W/L} $ 0.610 0.610 0.610 0.730 0.730 0.730 0.850 0.850 0.850 $\overline {T/W} $ 0.530 0.680 0.830 0.530 0.680 0.830 0.530 0.680 0.830 颗粒模型 
占比 P /% 2.1 3.5 1.5 5.4 2.9 0.7 1.9 0.7 0.2 序号 10 11 12 13 14 15 16 17 18 $ \overline{S\mathrm{_{_p}}} $ 0.925 0.925 0.925 0.925 0.925 0.925 0.925 0.925 0.925 $\overline {W/L} $ 0.610 0.610 0.610 0.730 0.730 0.730 0.850 0.850 0.850 $\overline {T/W} $ 0.530 0.680 0.830 0.530 0.680 0.830 0.530 0.680 0.830 颗粒模型 
占比 P /% 0.8 4.0 4.0 8.4 17.7 7.3 7.1 8.0 2.1 序号 19 20 21 22 23 24 25 26 27 $ \overline{S\mathrm{_{_p}}} $ 0.955 0.955 0.955 0.955 0.955 0.955 0.955 0.955 0.955 $\overline {W/L} $ 0.610 0.610 0.610 0.730 0.730 0.730 0.850 0.850 0.850 $\overline {T/W} $ 0.530 0.680 0.830 0.530 0.680 0.830 0.530 0.680 0.830 颗粒模型 — — — 
占比 P /% 0 0 0 0.6 4.0 4.9 1.7 6.0 4.2
下载: 导出CSV
表 3 仿真参数设置
Table 3. Simulation parameters setting
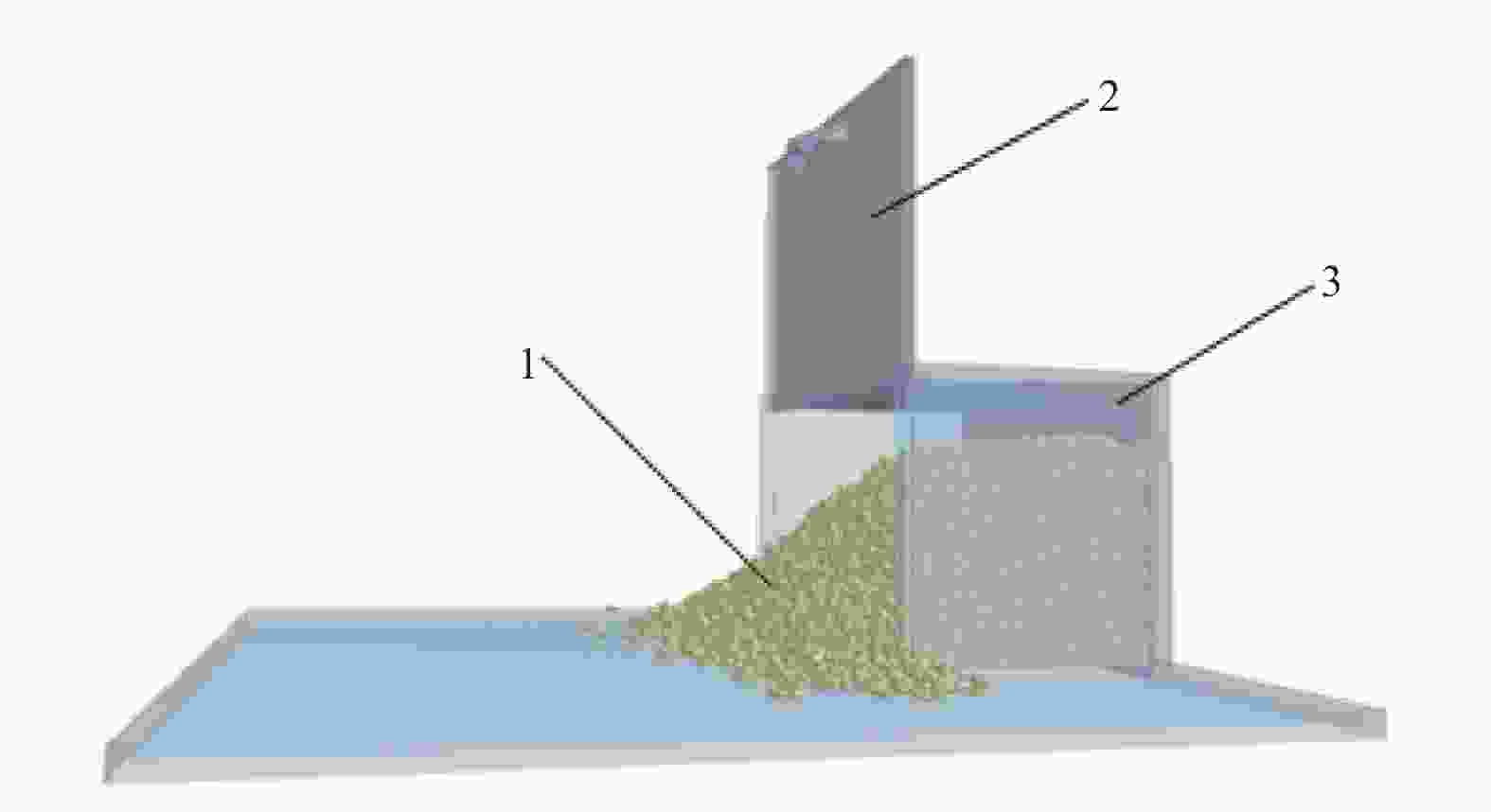
仿真参数 数值 核桃壳介质密度 $ {\rho _1} $/（kg·m−3） 1.024 × 103 核桃壳介质泊松比 μ1 0.29 核桃壳介质剪切模量 G1/Pa 9.219 × 107 亚克力板密度 $ {\rho _2} $/（kg·m−3） 1.200 × 103 亚克力板泊松比 μ2 0.50 亚克力板剪切模量 G2/Pa 1.770 × 108 核桃壳介质—亚克力板碰撞恢复系数 Cr 0.246 核桃壳介质—亚克力板静摩擦系数 μs 0.422 核桃壳介质—亚克力板滚动摩擦系数 μr 0.175 核桃壳介质间碰撞恢复系数 Cr' 0.340 核桃壳介质间静摩擦系数 μs' 0.720 ～ 0.920 核桃壳介质间滚动摩擦系数 μr' 0.020 ～ 0.200
下载: 导出CSV
表 4 仿真参数水平
Table 4. Parameter levels for simulation tests
水平 核桃壳介质间
静摩擦系数 X1核桃壳介质间
滚动摩擦系数 X2−2 0.720 0.020 −1 0.770 0.065 0 0.820 0.110 1 0.870 0.155 2 0.920 0.200
下载: 导出CSV
表 5 设计方案及结果
Table 5. Design scheme and results
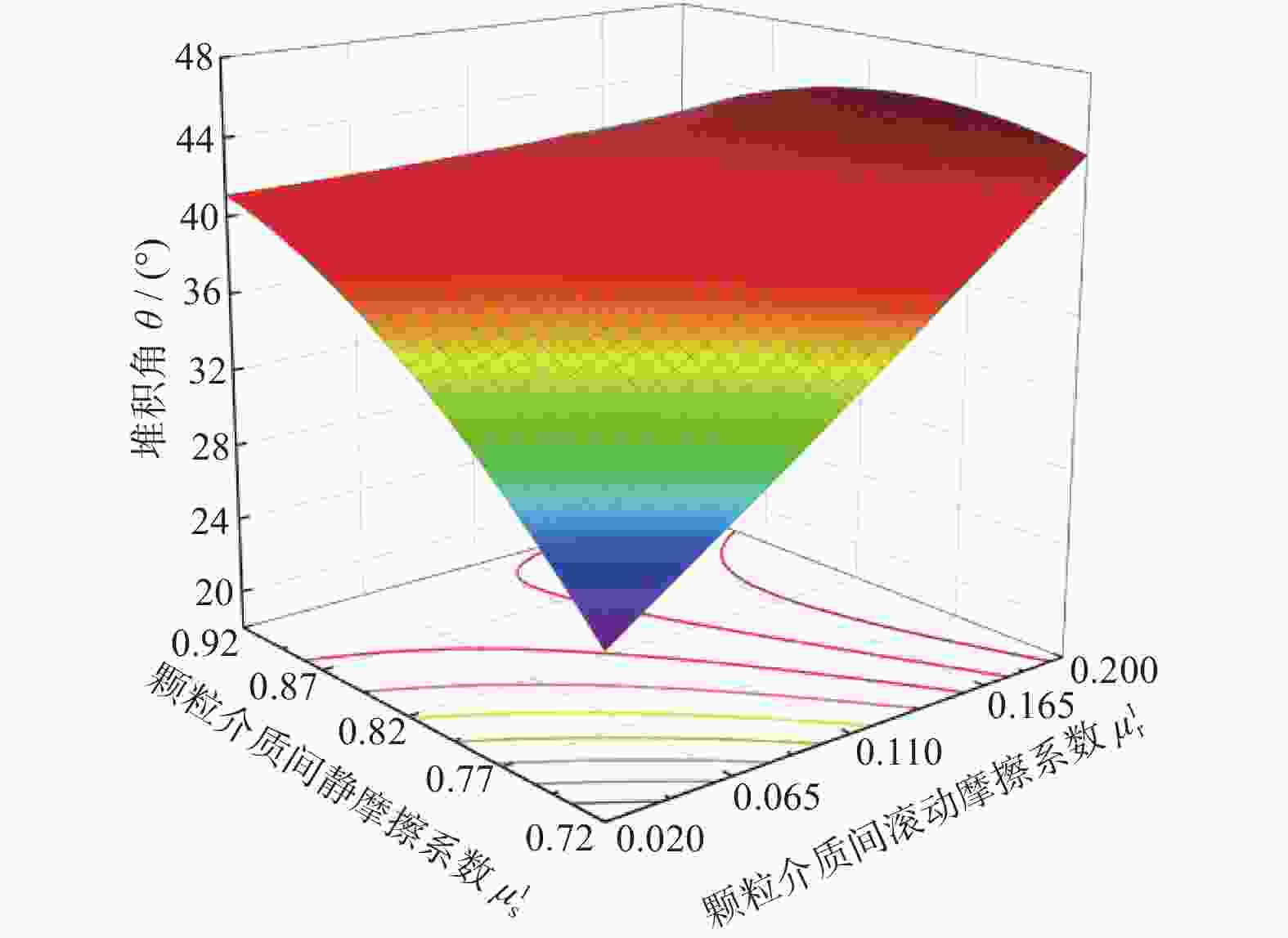
编号 因素 堆积角 θ /（°） X1 X2 1 −1 −1 35.15 2 1 −1 40.12 3 −1 1 41.45 4 1 1 42.12 5 −2 0 34.71 6 2 0 41.54 7 0 −2 35.63 8 0 2 45.51 9 0 0 39.93 10 0 0 40.23 11 0 0 40.38 12 0 0 40.17 13 0 0 41.21
下载: 导出CSV
表 6 二阶回归模型方差分析
Table 6. Second order regression model analysis of variance
方差源 平方和 SS 自由度 df 均方 MS P值 模型 109.70 5 21.94 <0.000 1 X1X1 10.76 1 14.62 0.000 3 X2X2 5.71 1 3.01 0.001 8 X1 X2 4.62 1 4.62 0.003 2 X12 7.32 1 10.77 0.010 5 X22 0.044 0 1 28.65 0.000 8 残差 1.68 7 0.898 0 失拟项 0.719 0 3 1.59 0.478 7 纯误差 0.957 9 4 0.378 6 总和 111.38 12
下载: 导出CSV
-
[1] 杨胜强, 李文辉, 李秀红, 等. 高性能零件滚磨光整加工的研究进展 [J]. 表面技术,2019,48(10):13-24. doi: 10.16490/j.cnki.issn.1001-3660.2019.10.002YANG Shengqiang, LI Wenhui, LI Xiuhong, et al. Research development of mass finishing for high-performance parts [J]. Surface Technology,2019,48(10):13-24. doi: 10.16490/j.cnki.issn.1001-3660.2019.10.002 [2] LI X H, LI W H, YANG S Q, et al. Study on polyurethane media for mass finishing process: Dynamic characteristics and performance [J]. International Journal of Mechanical Sciences,2018,138:250-261. doi: 10.1016/j.ijmecsci.2018.02.017 [3] WANG J M, LI X H, LI W H, et al. Research of horizontal vibratory finishing for aero-engine blades: Movement characteristics and action behavior of media [J]. The International Journal of Advanced Manufacturing Technology,2023,126(5):2065-2081. doi: 10.1007/s00170-023-11186-7 [4] 韩锐, 李秀红, 王嘉明, 等. 水平强制振动光整加工对TC4钛合金表面完整性参数的影响 [J]. 中国机械工程,2023,34(17):2037-2047. doi: 10.3969/j.issn.1004-132X.2023.17.003HAN Rui, LI Xiuhong, WANG Jiaming, et al. Influences of horizontal forced vibration finishing on surface integrity parameters of TC4 titanium alloys [J]. China Mechanical Engineering,2023,34(17):2037-2047. doi: 10.3969/j.issn.1004-132X.2023.17.003 [5] DAVIDSON D A. Green mass finishing with dry abrasive and polishing media novel finishing process allows refined surface edge effects while avoiding conventional wet-waste discharge [J]. Metal Finishing,2007,105(5):45-48. doi: 10.1016/S0026-0576(07)80551-4 [6] HERNANDEZ-GARCIA C, BULLARD D, HANNON F, et al. High voltage performance of a DC photoemission electron gun with centrifugal barrel-polished electrodes [J]. Review of Scientific Instruments,2017,88(9):093303. doi: 10.1063/1.4994794 [7] LV D J, WANG Y G, YU X, et al. Analysis of abrasives on cutting edge preparation by drag finishing [J]. The International Journal of Advanced Manufacturing Technology,2022,119(5):3583-3594. doi: 10.1007/s00170-021-08623-w [8] 李秀红, 王兴富, 杨英波, 等. 一种用于轴承滚动体表面的多仓超精离心抛磨装置及方法: CN114714239A [P]. 2022-07-08.LI Xiuhong, WANG Xingfu, YANG Yingbo, et al. A multi chamber ultra precision centrifugal polishing device and method for bearing rolling element surface: CN114714239A [P]. 2022-07-08. [9] 王键, 陆静. 寿山石的自动化拖拽抛光研究 [J]. 金刚石与磨料磨具工程,2020,40(4):53-58. doi: 10.13394/j.cnki.jgszz.2020.4.0008WANG Jian, LU Jing. Research on automatic draging-polishing of Shoushan stone [J]. Diamond & Abrasives Engineering,2020,40(4):53-58. doi: 10.13394/j.cnki.jgszz.2020.4.0008 [10] 王强, 李锻能, 廖伟东, 等. 二级行星磨料抛光机对矩形手机边框抛光实验研究 [J]. 机床与液压,2017,45(20):41-44. doi: 10.3969/j.issn.1001-3881.2017.20.011WANG Qiang, LI Duanneng, LIAO Weidong, et al. Experimental study on rectangular mobile frame by secondary planet abrasive polishing machine [J]. Machine Tool & Hydraulics,2017,45(20):41-44. doi: 10.3969/j.issn.1001-3881.2017.20.011 [11] 王志成, 李文辉, 李秀红, 等. 整体叶盘回转辅助水平振动式抛磨的颗粒力学行为仿真分析 [J]. 金刚石与磨料磨具工程,2022,42(5):617-625. doi: 10.13394/j.cnki.jgszz.2022.0051WANG Zhicheng, LI Wenhui, LI Xiuhong, et al. Simulation analysis of particle mechanical behavior in rotary-assisted horizontal vibration polishing of blisk [J]. Diamond & Abrasives Engineering,2022,42(5):617-625. doi: 10.13394/j.cnki.jgszz.2022.0051 [12] 张荔, 李文辉, 杨胜强. 滚磨光整加工中磨料颗粒堆积角的离散元参数标定 [J]. 中国科技论文,2016,11(16):1821-1825. doi: 10.3969/j.issn.2095-2783.2016.16.006ZHANG Li, LI Wenhui, YANG Shengqiang. Calibration of discrete element parameters of abrasive particle in mass finishing process [J]. China Sciencepaper,2016,11(16):1821-1825. doi: 10.3969/j.issn.2095-2783.2016.16.006 [13] LI X Y, DU Y F, LIU L, et al. Parameter calibration of corncob based on DEM [J]. Advanced Powder Technology,2022,33(8):103699. doi: 10.1016/j.apt.2022.103699 [14] PACHÓN-MORALES J, DO H, COLIN J, et al. DEM modelling for flow of cohesive lignocellulosic biomass powders: Model calibration using bulk tests [J]. Advanced Powder Technology,2019,30(4):732-750. doi: 10.1016/j.apt.2019.01.003 [15] LI L Z, BEEMER R D, ISKANDER M. Granulometry of two marine calcareous sands [J]. Journal of Geotechnical and Geoenvironmental Engineering,2021,147(3):04020171. doi: 10.1061/(ASCE)GT.1943-5606.0002431 [16] 李洪利, 吴文娟. 珊瑚礁砂颗粒形态研究 [J]. 土工基础,2023,37(4):667-671.LI Hongli, WU Wenjuan. Study on the particle morphology of the coral reef sand [J]. Soil Engineering and Foundation,2023,37(4):667-671. [17] 姜晓峰, 于维钊, 王继乾. 油水分离用天然材料表面化学研究进展 [J]. 化学通报,2021,84(4):290-304,321. doi: 10.14159/j.cnki.0441-3776.2021.04.001JIANG Xiaofeng, YU Weizhao, WANG Jiqian. The surface chemistry of natural materials for oil-water separation [J]. Chemistry,2021,84(4):290-304,321. doi: 10.14159/j.cnki.0441-3776.2021.04.001 [18] 何义川, 史建新. 核桃壳力学特性分析与试验 [J]. 新疆农业大学学报,2009,32(6):70-75. doi: 10.3969/j.issn.1007-8614.2009.06.016HE Yichuan, SHI Jianxin. Analysis and experiment on mechanical characteristic of walnut shell [J]. Journal of Xinjiang Agricultural University,2009,32(6):70-75. doi: 10.3969/j.issn.1007-8614.2009.06.016 [19] 黎展鹏, 刘凡一, 魏志强, 等. 茎瘤芥种子离散元模型参数标定 [J]. 中国农机化学报,2023,44(2):83-90. doi: 10.13733/j.jcam.issn.2095-5553.2023.02.012LI Zhanpeng, LIU Fanyi, WEI Zhiqiang, et al. Parameter calibration of discrete element model of stem mustard seeds [J]. Journal of Chinese Agricultural Mechanization,2023,44(2):83-90. doi: 10.13733/j.jcam.issn.2095-5553.2023.02.012 [20] 陈永, 高晓勋, 金鑫, 等. 油莎豆排种离散元仿真参数标定与试验 [J]. 农业机械学报,2023,54(12):58-69. doi: 10.6041/j.issn.1000-1298.2023.12.005CHEN Yong, GAO Xiaoxun, JIN Xin, et al. Calibration and analysis of seeding parameters of cyperus esculentus seedsbased on discrete element simulation [J]. Transactions of the Chinese Society for Agricultural Machinery,2023,54(12):58-69. doi: 10.6041/j.issn.1000-1298.2023.12.005 [21] 章广成, 向欣, 唐辉明. 落石碰撞恢复系数的现场试验与数值计算 [J]. 岩石力学与工程学报,2011,30(6):1266-1273.ZHANG Guangcheng, XIANG Xin, TANG Huiming. Field test and numerical calculation of restitution coefficient of rockfall collision [J]. Chinese Journal of Rock Mechanics and Engineering,2011,30(6):1266-1273. [22] 王刚, 王倩, 薛忠, 等. 基于离散元法的椰糠颗粒建模及仿真参数标定 [J]. 热带作物学报,2021,42(9):2704-2710. doi: 10.3969/j.issn.1000-2561.2021.09.036WANG Gang, WANG Qian, XUE Zhong, et al. Modeling and simulation parameters calibration of coconut coir particles based on DEM [J]. Chinese Journal of Tropical Crops,2021,42(9):2704-2710. doi: 10.3969/j.issn.1000-2561.2021.09.036 [23] 王万章, 刘婉茹, 袁玲合, 等. 基于EDEM的收获期小麦植株离散元参数标定 [J]. 河南农业大学学报,2021,55(1):64-72. doi: 10.16445/j.cnki.1000-2340.20210122.014WANG Wanzhang, LIU Wanru, YUAN Linghe, et al. Calibration of discrete element parameters of wheat plants at harvest period based on EDEM [J]. Journal of Henan Agricultural University,2021,55(1):64-72. doi: 10.16445/j.cnki.1000-2340.20210122.014 [24] 彭才望, 周婷, 孙松林, 等. 基于堆积试验的黑水虻离散元仿真参数标定与分析 [J]. 浙江农业学报,2022,34(4):814-823. doi: 10.3969/j.issn.1004-1524.2022.04.18PENG Caiwang, ZHOU Ting, SUN Songlin, et al. Calibration of parameters of black soldier fly in discrete method simulation based on response angle of particle heap [J]. Acta Agriculturae Zhejiangensis,2022,34(4):814-823. doi: 10.3969/j.issn.1004-1524.2022.04.18 [25] 葛越锋, 李小帅, 李春林, 等. 基于DEM的强制清种器清种性能研究 [J]. 拖拉机与农用运输车,2023,50(4):22-25.GE Yuefeng, LI Xiaoshuai, LI Chunlin, et al. Study on clearing performance of forced seed cleaner based on DEM [J]. Tractor & Farm Transporter,2023,50(4):22-25. [26] 郭娜, 姜新波, 纪欣鑫, 等. 青萝卜种子物性参数测定与离散元参数标定 [J]. 林业机械与木工设备,2023,51(9):25-32. doi: 10.3969/j.issn.2095-2953.2023.09.005GUO Na, JIANG Xinbo, JI Xinxin, et al. Determination of physical properties of green radish seeds and calibration of discrete element parameters [J]. Forestry Machinery & Woodworking Equipment,2023,51(9):25-32. doi: 10.3969/j.issn.2095-2953.2023.09.005 [27] 张胜伟, 张瑞雨, 陈天佑, 等. 绿豆种子离散元仿真参数标定与排种试验 [J]. 农业机械学报,2022,53(3):71-79. doi: 10.6041/j.issn.1000-1298.2022.03.007ZHANG Shengwei, ZHANG Ruiyu, CHEN Tianyou, et al. Calibration of simulation parameters of mung bean seeds using discrete element method and verification of seed-metering test [J]. Transactions of the Chinese Society for Agricultural Machinery,2022,53(3):71-79. doi: 10.6041/j.issn.1000-1298.2022.03.007 [28] 夏鹏, 李郁, 杨公波. 散粒物料堆积角离散元仿真研究 [J]. 起重运输机械,2015(2):107-110. doi: 10.3969/j.issn.1001-0785.2015.02.029XIA Peng, LI Yu, YANG Gongbo. Discrete element simulation study on pile angle of bulk material [J]. Hoisting and Conveying Machinery,2015(2):107-110. doi: 10.3969/j.issn.1001-0785.2015.02.029 -
点击查看大图
计量
- 文章访问数: 394
- HTML全文浏览量: 187
- PDF下载量: 7
- 被引次数: 0
邮件订阅
RSS
