Principle of self-assembly of abrasive balls on surface of grinding wheels into phyllotaxis arrangement
-
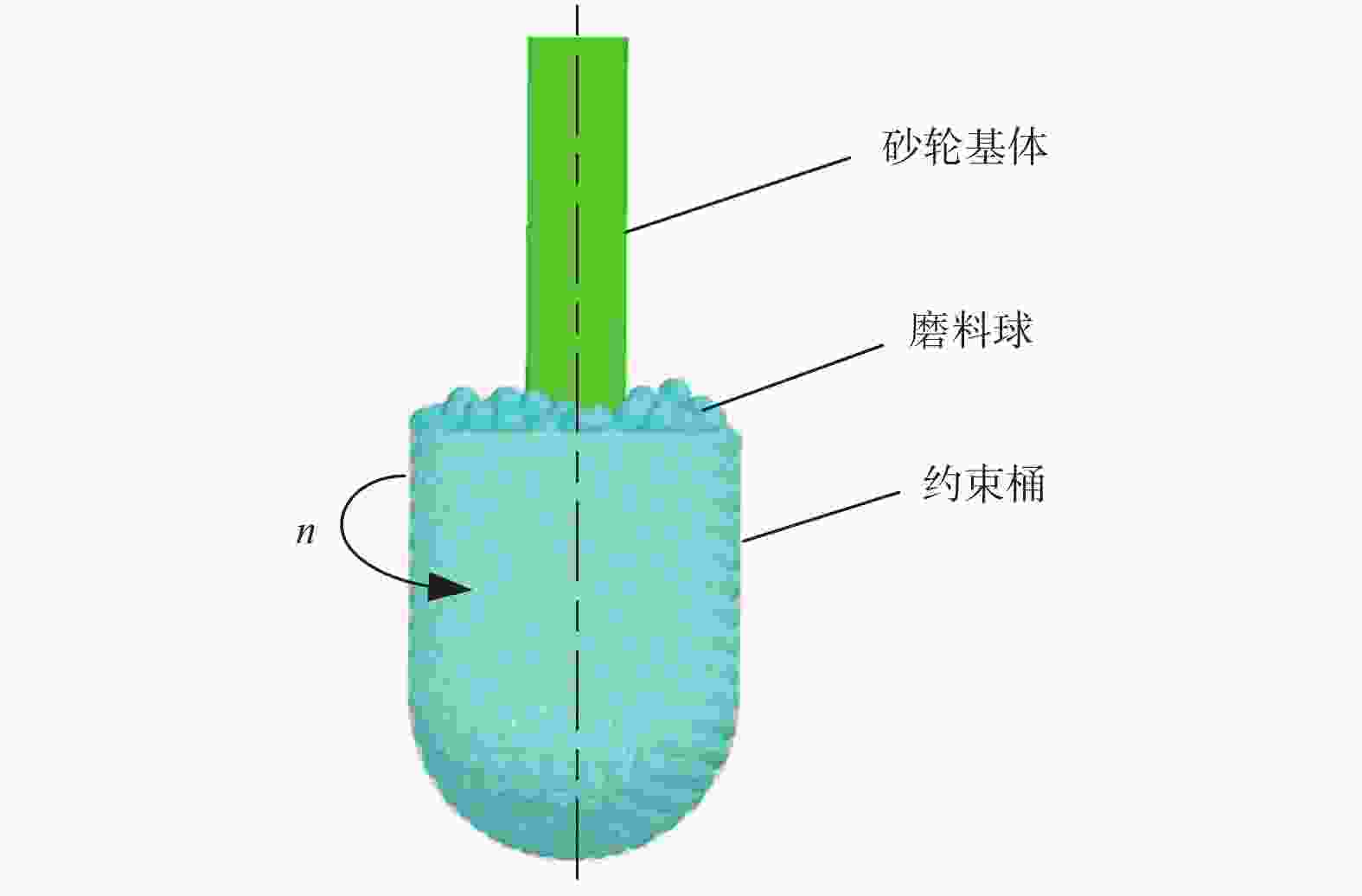
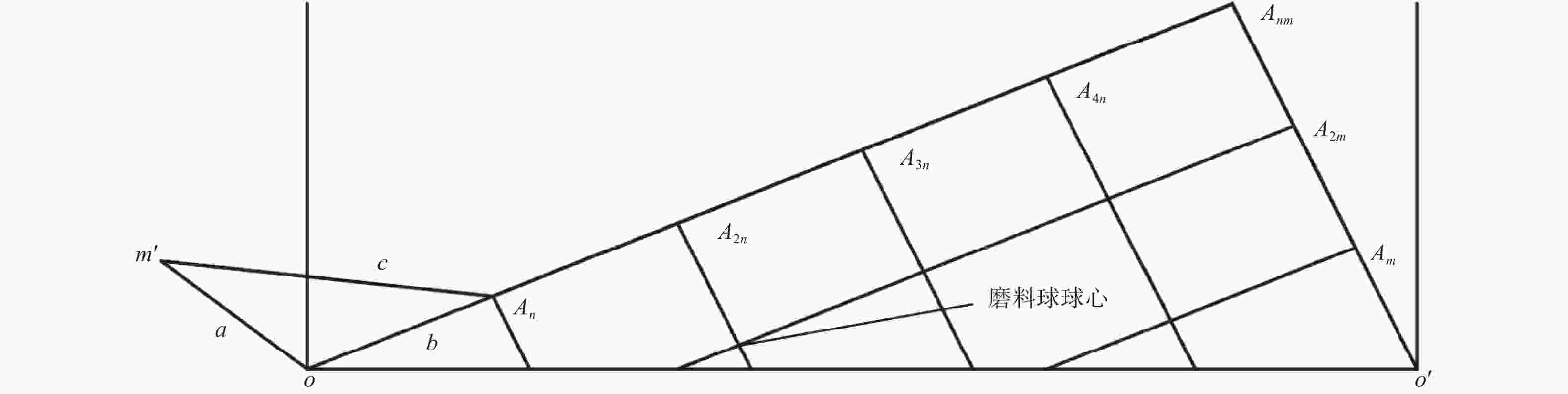
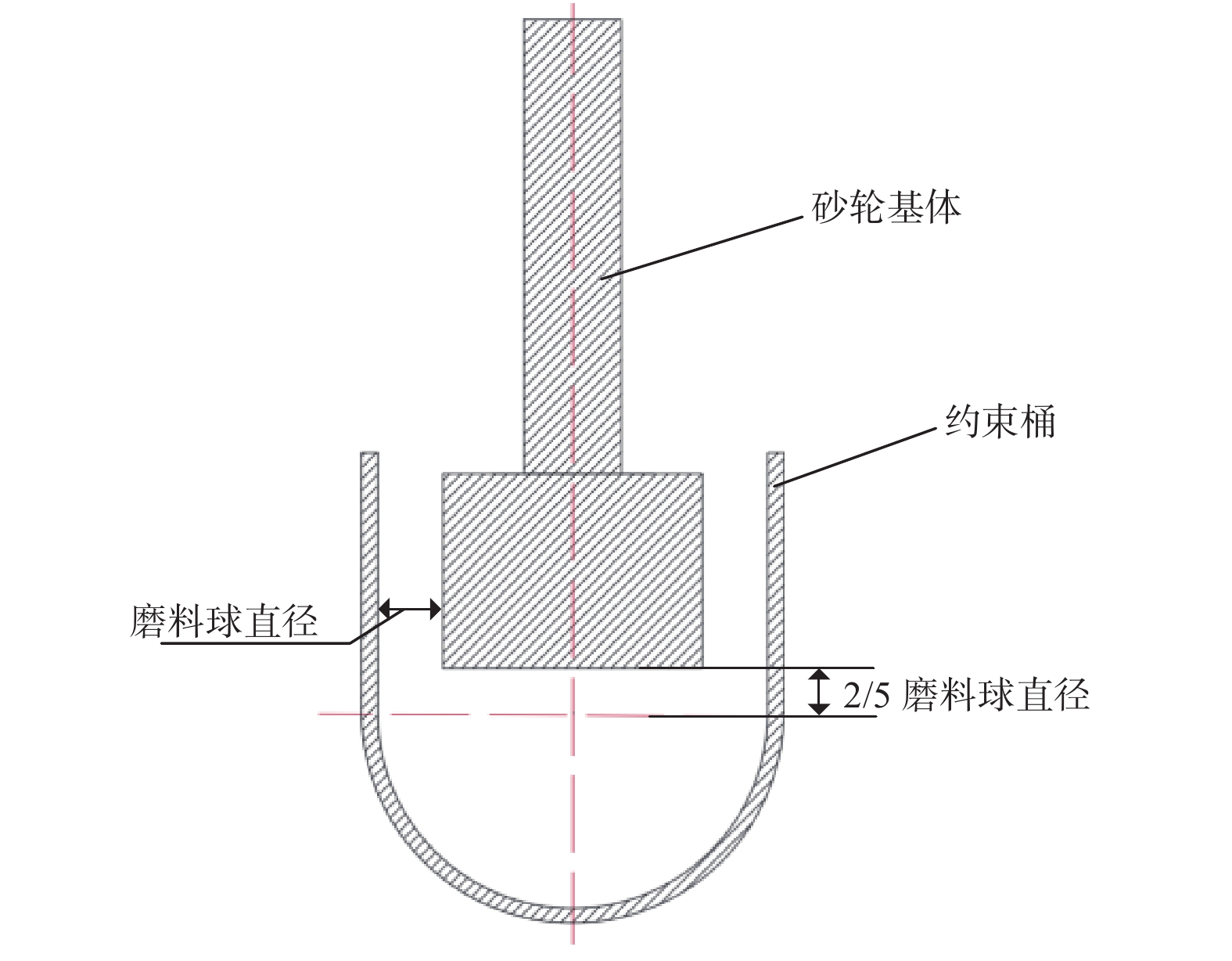
摘要: 为实现磨料球在砂轮基体表面有序化的自组装,提出一种叶序排布磨料球砂轮的自组装制造方法。从有界空间球体最密堆积结构原理与植物组织的柱面叶序结构理论出发,设计一种磨料球自组装砂轮的实验方法。首先对磨料球自组装过程进行仿真分析,然后探讨相关尺寸参数与自组装结构之间的关系,并经过计算得到不同尺寸参数下磨料球自组装结构。结果表明:通过自组装方法能实现磨料球在砂轮基体表面的叶序排布;当磨料球直径恒定时,磨料球在砂轮基体表面形成的叶序排布结构的叶序系数随着砂轮基体直径的增大而减小;当砂轮基体直径恒定时,磨料球在砂轮基体表面形成的叶序排布结构的叶序系数随着磨料球直径的增大而增大。Abstract: Objectives: Compared with traditional abrasive random arrangement grinding wheels, structured grinding wheels offer better chip space and grinding efficiency during the grinding process. At present, the manufacturing methods for structured grinding wheels mainly include metal sintering, electroplating, mechanical dressing, laser etching, and other processing techniques. However, these processing methods generally face several issues, such as low arrangement efficiency, poor positioning accuracy of abrasive particles, and complex manufacturing processes. To address these problems, this paper proposes a method for preparing an abrasive orderly grinding wheel by the orderly accumulation of abrasive balls in a bounded space. Methods: Phyllotactic arrangement refers to the arrangement of biological tissue units in space, such as rotation, opposition, and clustering, to provide an optimal growth environment for plant grains. The spiral arrangement achieves geometric spatial complementarity and maximizes the filling effect, with the left and right spirals formed by the arrangement satisfying the mathematical law of the Fibonacci sequence or its derived series. This paper, based on the theory of phyllotactic arrangement and the study of sphere packing structures in bounded spaces, establishes the basic theory for the self-assembly of abrasive spheres into an orderly arrangement on a grinding wheel. Results: Based on the growth structure characteristics of plant primordia, the constraint barrel in the device is designed to with a hemispherical bottom and a cylindrical top. To ensure that the abrasive balls on the surface of the grinding wheel are arranged in a single layer, the distance between the cylindrical part of the constraint bucket and the grinding wheel matrix is always equal to the diameter of a spherical particle. During the self-assembly process, the motion of the constraint barrel is used to mechanically disturb the absive balls. Due to the effects of gravity, interaction forces, and friction between the grinding balls, the arrangement structure of the grinding balls in the device gradually changes from random disorder to stable order. Once the structure stabilizes, the abrasive balls are fixed to the grinding wheel. Using the evaluation method of cylindrical phyllotaxis structure, multiple parallel oblique lines can be observed, and the distance between continuously growing primordia can be determined, allowing the relevant parameters of the phyllotaxis structure to be calculated. From the cylindrical coordinate expansion diagram and the cylindrical arrangement diagram, it is evident that multiple parallel left and right diagonals resemble the phyllotactic structure. Therefore, the structural parameters were verified and calculated. Conclusions: Abrasive ball-ordered grinding wheels with different grinding wheel matrix sizes were successfully prepared through self-assembly experiments. The abrasive ball arrangement structure was measured using corresponding measuring instruments to verify the accuracy of the self-assembly motion simulation results and the feasibility of the method. The influence of size changes on the structural parameters of the abrasive ball arrangement was discussed. The results indicate that the phyllotactic arrangement of spherical abrasives on the surface of the grinding wheel matrix can be achieved using the self-assembly method. When the diameter of the spherical abrasives is constant, the phyllotaxis coefficient of the arrangement structure formed by spherical abrasives on the surface of the grinding wheel substrate decreases with the increase of the diameter of the grinding wheel substrate. Conversely, when the diameter of the grinding wheel matrix is constant, the phyllotaxis coefficient of the phyllotaxis arrangement structure formed by the spherical abrasives on the surface of the grinding wheel substrate improves with the increase in the diameter of the abrasive balls.
-
Key words:
- structured grinding wheel /
- self-assembly /
- orderly arrangement /
- phyllotactic pattern /
- abrasive ball
-
表 1 磨料球与约束桶的材料特性
Table 1. Material properties of abrasice balls and confined barrels
物理参数 泊松比 μ 剪切模量 G / GPa 密度 ρ / (kg·m−3) 磨料球颗粒 0.30 105 2 400 约束桶 0.25 55 2 500 表 2 表面的接触特性
Table 2. Surface contact characteristics
接触参数 恢复系数 k1 静摩擦因数 k2 动摩擦因数 k3 球粒-球粒 0.10 0.30 0.01 球粒-桶 0.20 0.50 0.01 表 3 不同砂轮直径结构参数表
Table 3. Structure parameter table of different grinding wheel diameters
砂轮基体直径 D1 / mm 叶序模式 叶序系数 r 生长角 d / (°) 30 (9,7) 0.198 9 158.220 7 35 4(4,3) 0.182 0 154.547 0 40 (5,19) 0.159 9 74.604 6 45 5(3,4) 0.145 2 71.985 6 表 4 不同磨料球直径结构参数表
Table 4. Structure parameters of different abrasive ball diameters
磨料球直径 D2 / mm 叶序模式 叶序系数 r 生长角 d / (°) 4.5 (15,13) 0.156 6 167.173 0 5.5 (11,6) 0.227 4 62.821 5 6.5 (8,9) 0.454 1 42.924 8 7.0 (5,6) 0.480 2 63.607 4 表 5 不同砂轮直径结构参数表
Table 5. Structure parameter table of different grinding wheel diameters
砂轮基体直径 D1 / mm 叶序模式 叶序系数 r 生长角 d / (°) 30 (7,8) 0.213 1 161.780 4 35 5(3,2) 0.193 9 154.322 6 40 (5,19) 0.178 1 79.284 8 45 (14,19) 0.144 3 76.661 5 -
[1] DING W F, ZHU Y J, ZHANG L C, et al. Stress characteristics and fracture wear of brazed CBN grains in monolayer grinding wheels [J]. Wear,2015(332/333):800-809. doi: 10.1016/j.wear.2014.12.008 [2] BUTLER-SMITH P W, AXINTE D A, DAINE M. Preferentially oriented diamond micro-arrays: A laser patterning technique and preliminary evaluation of their cutting forces and wear characteristics [J]. International Journal of Machine Tools and Manufacture,2009,49(15):1175-1184. doi: 10.1016/j.ijmachtools.2009.08.007 [3] 谢国治, 左敦稳, 王珉. 单层钎焊砂盘磨粒分布有序性研究 [J]. 南京航空航天大学学报,2000(3):282-287. doi: 10.3969/j.issn.1005-2615.2000.03.007XIE Guozhi, ZUO Dunwen, WANG Min. Study on order distribution of monolayer brazing grindingplate’s grind grain [J]. Journal of Nanjing University of Aeronautics & Astronautics,2000(3):282-287. doi: 10.3969/j.issn.1005-2615.2000.03.007 [4] 郭兵, 金钱余, 赵清亮, 等. 表面结构化砂轮磨削加工技术研究进展 [J]. 哈尔滨工业大学学报,2016,48(7):1-13. doi: 10.11918/j.issn.0367-6234.2016.07.001GUO Bing, JIN Qianyu, ZHAO Qingliang, et al. Research progress of grinding technology with surface structured wheels [J]. Journal of Harbin Institute of Technology,2016,48(7):1-13. doi: 10.11918/j.issn.0367-6234.2016.07.001 [5] STEPIÉN P, SZAFARCZYK M. Generation of regular patterns on ground surfaces [J]. CIRP Annals,1989,38(1):561-566. doi: 10.1016/S0007-8506(07)62769-3 [6] 陈冰, 郭烨, 邓朝晖. 超硬磨粒可控排布砂轮研究进展 [J]. 中国机械工程,2023,34(9):1019-1034. doi: 10.3969/j.issn.1004-132X.2023.09.002CHEN Bing, GUO Ye, DENG Zhaohui. Research progresses of super-hard abrasive grain controllable arrangement grinding wheels [J]. China Mechanical Engineering,2023,34(9):1019-1034. doi: 10.3969/j.issn.1004-132X.2023.09.002 [7] 郭兵, 张庆贺, 郭振飞, 等. 基于结构化砂轮的结构表面高效精密磨削技术研究 [J]. 航空制造技术,2022,65(9):50-59. doi: 10.16080/j.issn1671-833x.2022.09.050GUO Bing, ZHANG Qinghe, GUO Zhenfei, et al. Research on high-efficiency precision grinding of structured surfaces based on structured grinding wheels [J]. Aeronautical Manufacturing Technology,2022,65(9):50-59. doi: 10.16080/j.issn1671-833x.2022.09.050 [8] 吕玉山, 王军, 赵成义, 等. 一种磨粒族叶序排布的端面砂轮及其铣磨实验 [J]. 兵工学报,2013,34(12):1569-1574. doi: 10.3969/j.issn.1000-1093.2013.12.012LYU Yushan, WANG Jun, ZHAO Chengyi, et al. An end-grinding wheel with the phyllotactic pattern of abrasive grain clusters and its mill-grinding experiments [J]. Acta Armamentarii,2013,34(12):1569-1574. doi: 10.3969/j.issn.1000-1093.2013.12.012 [9] RABIEY M, TAWAKOLI T, WEGENER K. The effect of special structured electroplated CBN wheel in dry grinding of 100Cr6 [J]. Advanced Materials Research,2009(76/77/78):119-124. doi: 10.4028/www.scientific.net/AMR.76-78.119 [10] TAWAKOLI T, RABIEY M. An innovative concept and its effects on wheel surface topography in dry grinding by resin and vitrified bond cbn wheel [J]. Machining Science and Technology,2008,12(4):514-528. doi: 10.1080/10910340802515989 [11] MOHAMED A M O, BAUER R, WARKENTIN A. Application of shallow circumferential grooved wheels to creep-feed grinding [J]. Journal of Materials Processing Technology,2013,213(5):700-706. doi: 10.1016/j.jmatprotec.2012.11.029 [12] LI H N, AXINTE D. Textured grinding wheels: A review [J]. International Journal of Machine Tools and Manufacture,2016,109:8-35. doi: 10.1016/j.ijmachtools.2016.07.001 [13] 王俊博, 吕玉山, 慕丽, 等. 磨粒有序化砂轮磨削微沟槽减阻表面的研究 [J]. 金刚石与磨料磨具工程,2022,42(6):738-744. doi: 10.13394/j.cnki.jgszz.2022.0031WANG Junbo, LYU Yushan, MU Li, et al. Effect of abrasive pattern on grinding micro-groove drag-reduction surface [J]. Diamond & Abrasives Engineering,2022,42(6):738-744. doi: 10.13394/j.cnki.jgszz.2022.0031 [14] LUO S Y, TU H Y, YU T H, et al. Grinding characteristics of micro-abrasive pellet tools fabricated by a LIGA-like process [J]. International Journal of Machine Tools and Manufacture,2009,49(3/4):212-219. doi: 10.1016/j.ijmachtools.2008.11.007 [15] 陈逢军, 张磊, 尹韶辉, 等. 基于静电喷雾的金刚石磨粒微表面均布特性研究 [J]. 表面技术,2018,47(7):15-20. doi: 10.16490/j.cnki.issn.1001-3660.2018.07.003CHEN Fengjun, ZHANG Lei, YIN Shaohui, et al. Uniform distribution characteristic of fine diamond abrasive particles based on high voltage electrostatic spraying [J]. Surface Technology,2018,47(7):15-20. doi: 10.16490/j.cnki.issn.1001-3660.2018.07.003 [16] MAO C, LONG P, TANG W D, et al. Simulation and experiment of electroplated grinding wheel with orderly-micro-grooves [J]. Journal of Manufacturing Processes,2022,79:284-295. doi: 10.1016/j.jmapro.2022.04.063 [17] 刘兆博, 吕玉山, 王军, 等. 磨粒族有序化排布砂轮磨削TC4的磨削力的实验研究 [J]. 机械设计与制造,2017,2017(2):115-117. doi: 10.3969/j.issn.1001-3997.2017.02.032LIU Zhaobo, LYU Yushan, WANG Jun, et al. Experimental investigation on the grinding force of the abrasive cluster engineered grinding wheel in grinding TC4 [J]. Machinery Design & Manufacture,2017,2017(2):115-117. doi: 10.3969/j.issn.1001-3997.2017.02.032 [18] MORONUKI N, ZHANG W R. Patterned self-assembly of fine particles and its application to polishing tool [J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing,2012,6(6):792-799. doi: 10.1299/jamdsm.6.792 [19] 龚胜, 王永强, 尹韶辉, 等. 应用环形磁场控制的微粉砂轮制备及其磨削性能 [J]. 机械工程学报,2016,52(17):78-85. doi: 10.3901/JME.2016.17.078GONG Sheng, WANG Yongqiang, YIN Shaohui, et al. Fabrication of fine grinding wheel controlled by annular magnetic field and its grinding performance [J]. Journal of Mechanical Engineering,2016,52(17):78-85. doi: 10.3901/JME.2016.17.078 [20] JEAN R V. Phyllotactic pattern generation: A conceptual model [J]. Annals of Botany,1988,61(3):293-303. doi: 10.1093/oxfordjournals.aob.a087557 [21] MUGHAL A, CHAN H K, WEAIRE D, et al. Dense packings of spheres in cylinders: Simulations [J]. Physical Review, E. Statistical, Nonlinear, and Soft Matter Physics,2012,85(5):1-17. doi: 10.1103/PhysRevE.85.051305 [22] PATANKAR A N, MANDAL G. The packing of solid particles: A review [J]. Transactions of the Indian Ceramic Society,1980,39(4):109-119. doi: 10.1080/0371750X.1980.10840732 [23] VAKARELOV I. Method for practical assessment of cylindrically represented spiral phyllotaxis [J]. Phytologia Balcanica,2008,14(2):263-268. [24] 李兴山, 熊伟, 陈天宇, 等. 磨粒簇叶序排布砂轮外圆磨削凹坑结构化减阻表面的仿真 [J]. 机械设计与制造,2021(3):261-265. doi: 10.3969/j.issn.1001-3997.2021.03.059LI Xingshan, XIONG Wei, CHEN Tianyu, et al. Simulation study on the grinding of cylindrical structured surface by the grinding wheel with phyllotactic abrasive cluster [J]. Machinery Design & Manufacture,2021(3):261-265. doi: 10.3969/j.issn.1001-3997.2021.03.059 -




 下载:
下载:





 邮件订阅
邮件订阅 RSS
RSS
